基于斜率分布的离散波形数据压缩方法与流程
发明涉及属于数据压缩的技术领域,具体涉及一种基于斜率分布的离散波形数据压缩新方法。
背景技术:
波形数据在工业领域的设备监测中占有非常重要的地位,以电力系统为例,很多监测系统均采用波形数据展开对电力设备的监测,比如变压器、断路器、避雷器、绝缘子等等,均通过波形信号展开对其状态的诊断。
采用波形信号监测工业设备的过程中会产生大量数据。以电力系统中的绝缘子为例,可以采用泄漏电流波形信号诊断绝缘子的状态,但是,污秽绝缘子在潮湿情况下会产生大量的报警波形数据,而输电线路上绝缘子众多,一旦发生雨雪天气,同一时间段内产生的波形数据将非常巨大,这对数据传输和存储都提出了极高的要求。因此,提高数据传输效率和增强数据存储能力成为一项必要的措施。
数据压缩方法可以将原始的数据压缩为相对较少的数据,可以有效提高数据传输的有效性和增强存储空间的利用率。数据压缩方法分为无损压缩和有损压缩,采用前者方法压缩信号之后的成分不会发生损失;采用后者方法压缩信号之后成分有所取舍。由于有损压缩舍掉了其中一部分成分,所以,往往压缩效果更好。若在保证不影响信号分析效果的前提下,有损压缩成为一种很好的方法。
当前,已存在许多压缩方法,比如,直接对原始信号采用rle(runlengthencoding)方法进行压缩;再比如,采用小波变换的方法将原始信号变换到时频域后,采用适当的编码方案实现信号的压缩。不同的压缩方法适用于不同特征的信号,即,为了实现更佳的压缩效果,不同的信号应根据自身特点,选择更好的压缩方法。
技术实现要素:
本发明的目标是提供一种压缩离散波形数据的新方法,以便提高传输通道和存储空间的利用率。为此本发明专利中提出了一种适合于压缩离散波形数据的方法,该方法根据离散波形信号的斜率分布,选择少数斜率值作为依据,构建各个线段,达到逼近原始信号的目的,从而实现离散波形信号的压缩。
本发明提供了一种基于斜率分布的离散波形数据压缩方法,其特征在于所述方法包括如下步骤:
步骤1:将原始离散波形数据转换为斜率序列;
步骤2:根据斜率序列的分布,选择m个类别中心;
步骤3:以各类的类别中心为斜率值,逼近原始离散波形中各相邻点之间的线段,所有线段连接在一起,实现逼近整个离散波形的目的,从而实现原始离散波形的稀疏表示;
步骤4:采用哈夫曼方法对原始离散波形的稀疏表示进行压缩编码,实现信号的最终压缩处理。
进一步地,所述步骤1包括下列步骤:
步骤11:采集待分析的离散波形数据,设其长度为n,并令i=1;
步骤12:若i≤n-1,转步骤13,否则转步骤16;
步骤13:取波形上的相邻数据点(xi,yi)和(xi+1,yi+1),两点构成一条线段,令该线段所在的直线为li;
步骤14:计算直线li的斜率
步骤15:i=i+1,转步骤12;
步骤16:构造集合s={l1,l2,…,ln-1}。
进一步地,所述步骤3包括下列步骤:
步骤31:令斜率序列组成的集合为r={},令逼近原始离散波形的新坐标集合v={},取原始离散波形的坐标值(xi,yi),此处i=1,并取v=v∪{(xi,yi)};
步骤32:令j=1;
步骤33:若j≤m,转步骤34,否则转步骤36;
步骤34:计算截距bj=yi-cj×xi和逼近之后的纵坐标yji+1=cj×xi+1+b;
步骤35:j=j+1,转步骤33;
步骤36:取min(abs(yji+1-yi+1)),其中,j=1,2,…,m,并记此时对应的斜率为ck,将yji+1赋值给yi+1;
步骤37:更新集合r=r∪{ck},v=v∪{(xi+1,yi+1)};
步骤38:令i=2,若i<n,则转步骤32,否则转步骤39;
步骤39:求得的r为逼近原始离散波形所用的斜率序列,求得的v为新波形的坐标序列。
本发明的基于斜率分布的离散波形数据压缩方法,适用于解决离散波形数据在传输中需要较大带宽和在存储中需要较大空间的问题,通过该方法可以有效降低数据传输带宽和数据存储空间,达到提高利用率的目的。
附图说明
为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例描述中所需要使用的附图作一简单地介绍。显而易见地,下面描述中的附图是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。
图1为根据本发明的实验原理图;
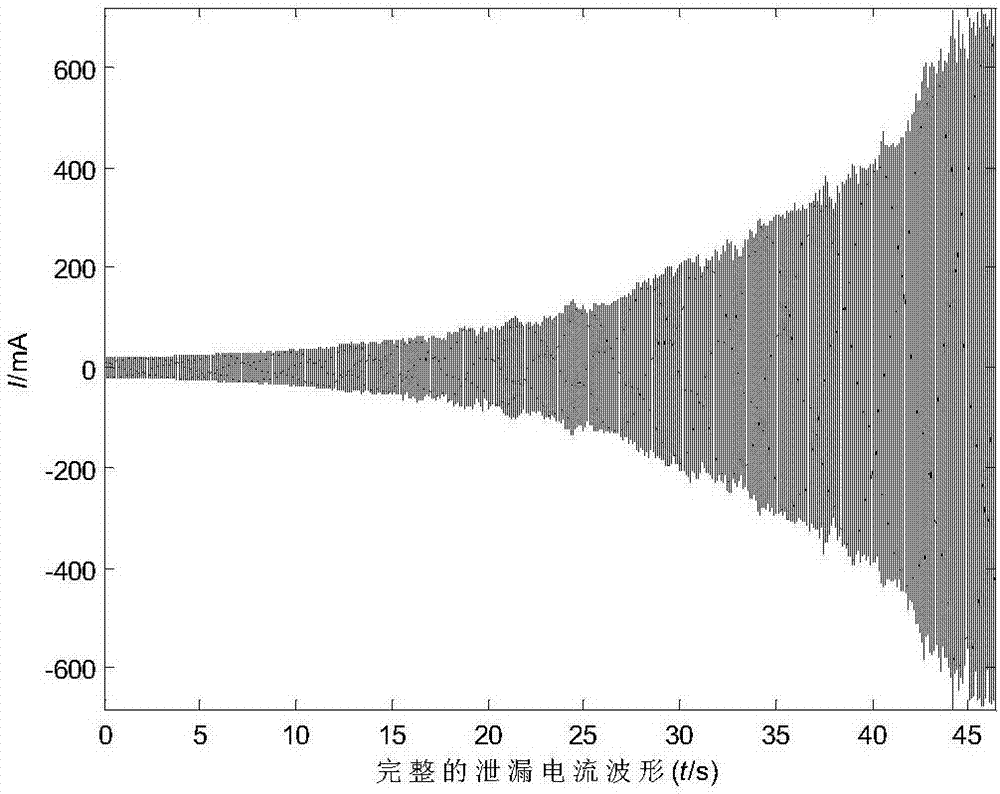
图2为根据本发明的实验中采集到的完整泄漏电流波形图;
图3为根据本发明的泄漏电流波形图;
图4为根据本发明的选择7个斜率时的哈夫曼树;
图5为根据本发明的选择7个斜率时解压后的波形图;
图6为根据本发明的原始波形的频谱和选择7个斜率时压缩后的频谱;
图7为根据本发明的选择5个斜率时的哈夫曼树;
图8为根据本发明的选择5个斜率时解压后的波形图;
图9为根据本发明的原始波形的频谱和选择5个斜率时压缩后的频谱;
图10为根据本发明的选择3个斜率时的哈夫曼树;
图11为根据本发明的选择3个斜率时解压后的波形图;
图12为根据本发明的原始波形的频谱和选择3个斜率时压缩后的频谱。
具体实施方式
方法的基本思路是:首先,将原始离散波形数据转换为斜率序列,即,取原始离散数据波形相邻点所在直线的斜率值,并由这些斜率值组成一个集合,求所有斜率值的目的是为了确定少数代表性斜率值,为压缩打下基础;其次,根据斜率序列的分布,选择若干个类别中心,将其作为代表性斜率值;再次,在误差允许的范围内,由各代表性斜率值逼近原始离散数据波形中各相邻点的线段,并将各个线段连接在一起,实现对原始离散波形的逼近,进而实现原始离散波形数据的稀疏表示;然后,对原始离散波形数据的稀疏表示进行压缩编码,实现波形信号的压缩处理;最后,对信号进行分析时,对压缩编码进行解压,并恢复用于逼近原始离散波形的数据。
本发明的技术方案为:基于斜率分布的离散波形数据压缩新方法包括如下步骤:
步骤1:将原始离散波形数据转换为斜率序列;
步骤2:根据斜率序列的分布,选择m个类别中心;
步骤3:以各类的类别中心为斜率值,逼近原始离散波形中各相邻点之间的线段,所有线段连接在一起,实现逼近整个离散波形的目的,从而实现原始离散波形的稀疏表示;
步骤4:采用哈夫曼方法对原始离散波形的稀疏表示进行压缩编码,实现信号的最终压缩处理;
步骤5:对信号进行分析时,对压缩编码进行解压,并恢复用于逼近原始离散波形的数据。
所述步骤1包含以下步骤:
步骤11:采集待分析的离散波形数据,设其长度为n,并令i=1;
步骤12:若i≤n-1,转步骤13,否则转步骤16;
步骤13:取波形上的相邻数据点(xi,yi)和(xi+1,yi+1),两点构成一条线段,令该线段所在的直线为li;
步骤14:计算直线li的斜率
步骤15:i=i+1,转步骤12;
步骤16:构造集合s={k1,k2,…,kn}表示斜率序列。
所述步骤2包含以下步骤:
步骤21:根据压缩的要求选择类别数,记为m;
步骤22:采用kmeans聚类算法,将集合s中的元素分为m类,计算每类的平均值,并将其设为类别中心,,记为cj,j=1,2,…,m,并令集合c={c1,c2,…,cm}。
所述步骤3包含以下步骤:
步骤31:令斜率序列组成的集合为r={},令逼近原始离散波形的新坐标集合v={},取原始离散波形的坐标值(xi,yi),此处i=1,并取v=v∪{(xi,yi)};
步骤32:令j=1;
步骤33:若j≤m,转步骤34,否则转步骤36;
步骤34:计算截距bj=yi-cj×xi和逼近之后的纵坐标yji+1=cj×xi+1+b;
步骤35:j=j+1,转步骤33;
步骤36:取min(abs(yji+1-yi+1)),其中,j=1,2,…,m,并记此时对应的斜率为ck,将yji+1赋值给yi+1;
步骤37:更新集合r=r∪{ck},v=v∪{(xi+1,yi+1)};
步骤38:令i=2,若i<n,则转步骤32,否则转步骤39;
步骤39:求得的r为逼近原始离散波形所用的斜率序列,求得的v为新波形的坐标序列。
所述步骤4包含以下步骤:
步骤41:统计集合c中各个元素在集合r中出现的次数wj(j=1,2,…,m),并令集合w={w1,w2,…,wm};
步骤42:为集合中w构造哈夫曼树t;
步骤43:根据哈夫曼树t,为集合r构造压缩编码。
所述步骤42包含以下步骤:
步骤421:根据集合w构造哈夫曼树的初始集合t={t1,t2,…,tm},其中,每棵二叉树ti中包含斜率值ci及其权值wi的根结点,它的左右子树均为空;
步骤422:如果集合t中只有一个元素,则转步骤425,否则转步骤423;
步骤423:在集合t中选取两个根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根节点的权值为其左右子树的根节点的权值之和;
步骤424:从集合t中删除上述两棵树,并把新二叉树的根结点权值加入集合t中,并转步骤422;
步骤425:令集合a={},并取a=a∪t;
步骤426:若a≠{},则转步骤427,否则转步骤4212;
步骤427:从a中取元素ti,若该结点的左子树不为空则转步骤428,否则转步骤429;
步骤428:令ti的左子树为tj,则在集合t中将ti指向tj的连线上设置标号0,并计算a=a∪{tj};
步骤429:若结点ti的右子树不为空,则转步骤4210,否则转步骤4211;
步骤4210:令ti的右子树为tk,则在集合t中将ti指向tk的连线上设置标号1,并计算a=a∪{tk};
步骤4211:计算a=a-{ti},并转步骤426;
步骤4212:得到最终的哈夫曼树,其中,每个叶子结点包含一个斜率值及其权值,从根结点到该叶子结点的所有连线上的标号序列即为该叶子结点的编码。
所述步骤43包含以下步骤:
步骤431:令编码串
步骤432:若集合r≠{},则转步骤433,否则转步骤435;
步骤433:从r中取一个元素,并在哈夫曼树t中查找对应该元素的叶子结点,并得到该元素的编码zi,并令z=z+zi(此处的“+”表示连接);
步骤434:从集合中删除该元素,并转步骤432;
步骤435:编码串z即为压缩编码,结束。
所述步骤5包含以下步骤:
步骤51:求解解压后的斜率序列;
步骤52:利用原始离散波形的第一个数据点和解压后的斜率序列,构造用于逼近原始离散波形的数据。
所述步骤51包含以下步骤:
步骤511:令集合r={};
步骤512:若length(z)≠0,转步骤513,否则转步骤515,其中,函数length表示取长度;
步骤513:从编码串z的起始位置开始,查找第一个能和哈夫曼树中某个叶子结点一致的编码,并取该结点对应的斜率值cj;
步骤514:计算r=r∪{cj},并将z中已识别的编码去掉,转步骤52;
步骤515:最终得到的集合r就是解压后的斜率序列,结束。
所述步骤52包含以下步骤:
步骤521:取原始离散波形的第一个数据点,将其坐标赋给(xi,yi),并令i=1,集合x=x∪{(xi,yi)};
步骤522:若r≠{},转步骤523,否则转步骤527;
步骤523:取r中第一个元素对应的斜率值cj,并计算r=r-{cj};
步骤524:计算截距b=yi-cj×xi;
步骤525:计算下一个相邻数据点的坐标,设等间隔采样,并令采样间隔为d,则下一个数据点的横坐标xi+1=xi+1,纵坐标yi+1=cj×xi+1+b;
步骤526:计算x=x∪{(xi+1,yi+1)},计算i=i+1,转步骤522;
步骤527:最终得到的集合x就是解压后的数据集合,结束。
本方法与现有方法的区别在于:
本发明所提的方法为有损压缩,与现有的有损压缩方法的显著区别是:从一种全新的视角对离散波形的压缩展开研究,具体来说,将数据波形变换为斜率序列进行压缩,这是以往方法未曾提到过的。现有的对波形进行有损压缩的典型方法有很多,比如:多项式拟合法、均匀抽样插值法、基于小波变换的压缩方法等。其中,多项式拟合法在波形长度增加、波形较复杂的情况下,难以获得满意的拟合结果,会产生较大的误差;均匀抽样插值法在抽样的过程中可能会丢失重要的特征点,从而无法准确反映数据特征;基于小波变换的压缩方法虽然能够取得较好的效果,但需要解决一些列问题,比如选择最佳小波基、选择最佳阈值、选择小波分解的层数等等,这都增加了压缩的困难。本发明所提的方法避免了上述方法的缺陷,实现有效压缩。
为了验证本发明算法的有效性,采用所提的方法对实验中采集的波形数据进行压缩。实验中,采集输电线路绝缘子泄漏电流的试验在人工雾室环境下进行,具体的原理如图1所示。高压线路通过保护电阻穿过套管与人工气候室内的绝缘子串连接,同时通过电容分压器进行分压,后部通过测量装置和泄漏电流传感器进行测量。其中,选择的绝缘子的型号为fxbw4-110/100。试验中采用涂层染污方式,并用硅藻土模拟不溶性物质,用氯化钠模拟可溶性物质,通过涂刷方式将污秽物涂于绝缘子表面。污秽物的等值盐密ρesdd=0.1mg/cm2,灰密ρnsdd=0.5mg/cm2。试验过程中采用升压法展开数据的采集工作,且相对湿度设置为90%、温度设置为27℃。在采样频率为10khz的情况下,如图2所示为试验过程中采集到的完整泄漏电流波形。为了对信号展开分析,截取一部分典型的波形如图3所示,该波形包含了1000个数据点。
根据上述所属步骤,将图3的数据波形变换为斜率序列。
首先,选择7个类别中心,此处各个类别中心分别设置为:-3/2、-1、-1/2、0、1/2、1、3/2。对图3的波形进行压缩时,各个斜率出现的次数如表1所示。
表1各斜率值出现的次数
按照表1构建哈夫曼树,如图4所示。按照图4的哈夫曼树对波形进行压缩编码。若压缩前数据按double类型存储,而double类型的长度为4个字节(32位),则压缩前和压缩后数据占的位数如表2所示。
表2编码前和编码后数据占的位数
即,压缩前数据占用的空间是压缩后的约10.7倍,即取得了很客观的压缩效果。
对压缩编码进行解压,并恢复逼近原始离散波形的数据,如图5所示。原始离散波形和解压后波形的频谱如图6所示,其中图6(a)为原始离散波形的频谱,图6(b)为解压后波形的频谱。由图3和图5的比较可以看出,压缩方法对波形数据的影响很小;由图6(a)和图6(b)的比较可以看出,主要的周期成分都得到了保留。
其次,选择5个类别中心,此处各个类别中心分别设置为:-3/2、-1/2、0、1/2、3/2。对图3的波形进行压缩时,各个斜率出现的次数如表3所示。
表3各斜率值出现的次数
按照表3构建哈夫曼树,如图7所示。按照图7的哈夫曼树对波形进行压缩编码。若压缩前数据按double类型存储,而double类型的长度为4个字节(32位),则压缩前和压缩后数据占的位数如表4所示。
表4编码前和编码后数据占的位数
即,压缩前数据占用的空间是压缩后的约13.7倍,压缩比进一步扩大。
对压缩编码进行解压,并恢复逼近原始离散波形的数据,如图8所示。原始离散波形和解压后波形的频谱如图9所示,其中图9(a)为原始离散波形的频谱,图9(b)为解压后波形的频谱。由图3和图8的比较可以看出,压缩方法对波形数据的影响较小;由图9(a)和图9(b)的比较可以看出,主要的周期成分都得到了保留。
再次,选择3个类别中心,此处各个类别中心分别设置为:-1/2、0、1/2。对图3的波形进行压缩时,各个斜率出现的次数如表5所示。
表5各斜率值出现的次数
按照表5构建哈夫曼树,如图10所示。按照图10的哈夫曼树对波形进行压缩编码。若压缩前数据按double类型存储,而double类型的长度为4个字节(32位),则压缩前和压缩后数据占的位数如表6所示。
表6编码前和编码后数据占的位数
即,压缩前数据占用的空间是压缩后的约20.2倍,压缩比进一步扩大。
对压缩编码进行解压,并恢复逼近原始离散波形的数据,如图11所示。原始离散波形和解压后波形的频谱如图12所示,其中图12(a)为原始离散波形的频谱,图12(b)为解压后波形的频谱。由图3和图11的比较可以看出,压缩方法对波形数据的影响较小,且在一定程度上去除了部分噪声,平滑了波形;由图12(a)和图12(b)的比较可以看出,主要的周期成分都得到了保留。
由上述3次选择不同的斜率组合进行压缩的结果可以看出,不同的斜率组合的压缩比不同。当压缩比要求较高时,可以选择较少的斜率值进行压缩;反之,选择较多的斜率值。由压缩后的波形及其频谱可以看出,当在保留主要分析成分的前提下,选择较少的斜率值进行压缩,不影响分析效果。
本发明的压缩方法可以根据要求灵活选择压缩比,达到更佳的压缩效果。
- 还没有人留言评论。精彩留言会获得点赞!